Blackjack & Deep Q Learning

Dec 20, 2023 • 14 min read

This largely builds off off my previous post here. While I outlined a Q Learning approach to training a blackjack RL agent, I'll extend it to neural networks and a Deep Q Learning implementation. While I showed that blackjack, without card count, is a tractable problem for Q learning where we memorize all state-action pairs, this becomes a largely infeasible task when the action/state space expands. Even if we don't expand the state-action space, I wonder what type of performance we can achieve with this new approach.

Why Deep Q Learning?

In the Q Learning approach, we determine the Q function explicitly and require access to all state-action pairs in order to do so. Think of it as a lookup table. If our state-action space expands, this becomes intractable entirely. Imagine in the Q Learning approach, where our state-action space looked like this:

Q[(10, 4, false)] = {
  "hit": 0,
  "stay": 0,
  "double": 0,
  "split": 0,
  "surrender": 0,
}

What if we wanted to add running card count to the state? What if we wanted to add true count to the state? It might look something like this

Q[(10, 4, false, +1.321)] = {
  "hit": 0,
  "stay": 0,
  "double": 0,
  "split": 0,
  "surrender": 0,
}

While we can sacrifice some precision in that true count state variable in order to reduce the number of states, you can imagine that we'd run into issues where the state-action space expands too drastically to store in memory. Even if we were able to store these in memory, we'd have to visit each of these highly specific states incredibly often in order to learn the appropriate Q values. Also, what if we add additional decks and observe new card counts that our model didn't observe during training?

Given state and action $s$, $a$
Q Learning:
Look up $Q(s,a)$

Deep Q Learning:
Compute $Q ≈ f(state) → Q[a]$

Neural networks fix this issue. Rather than explicitly learning this Q function for every possible state-action pair, we can learn an approximation for this Q function.

A depiction of the comparisons between Q Learning methods and Deep Q Learning methods.

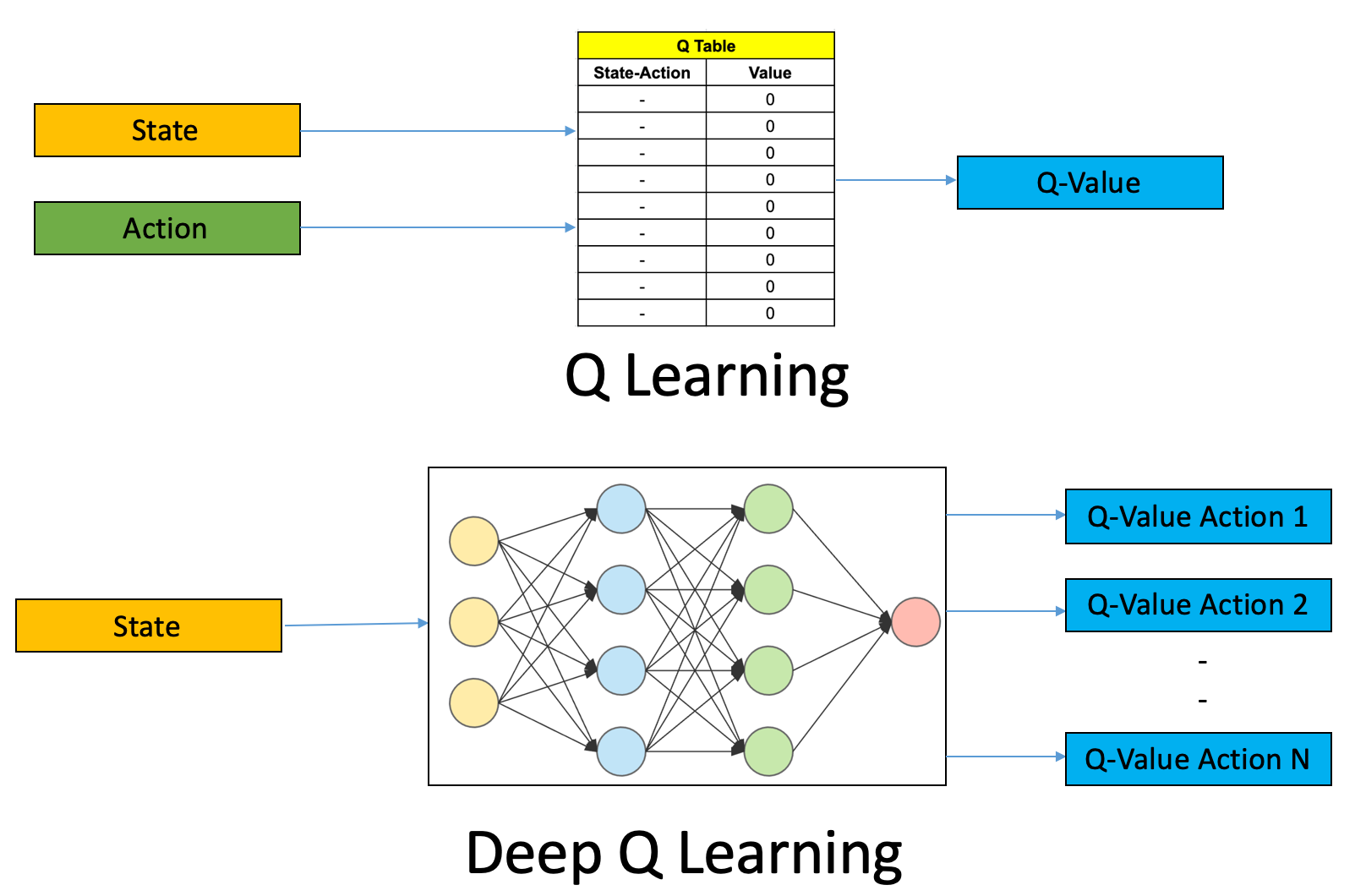
Deep Q Learning

Feed-forward neural networks trained in a supervised manner require ground truth targets to train on. In reinforcement learning, we don't quite have these ground truth targets, as our objective is to learn some function that maximizes our expected reward, whatever the steps to achieve that might entail, we just don't know yet.

Our objective changes when extending Q Learning to Deep Q Learning. Instead of learning the Q function explicitly, we can approximate the Q function by minimizing the MSE (or Huber Loss) between Temporal Difference Q values of current and future states. Ultimately, we are regressing the Q value for each possible action for a given state compared with future Q values and rewards. As this neural network approximation for Q can theoretically learn any function through a use of linear and non-linear layers, we should be able to achieve our desired results.

Remember our update step in Q learning:

Maybe it's more intuitive to write this as the following to more explicitly detail the "Temporal Difference" piece of this equation.

Let's break this down further. The discounted estimate of optimal Q value of next state is:

$\gamma * max_a(Q(s_{t+1},a_{t+1}))$

The Temporal Difference Target is:

$TD_{target}(s_{t+1},a_{t+1}) = R_{t+1} + \gamma * max_a(Q(s_{t+1},a_{t+1}))$

We know the current Q value estimate, so we can specify the TD Error:

$TD(s_t,a_t) = TD_{target}(s_{t+1},a_{t+1}) - Q(s_t,a_t)$

Where our specific aim is to iteratively learn $Q(s,a)$, such that for a given timestep:

$Q(s_t,a_t) = Q(s_t,a_t) + lr * TD(s_t,a_t)$

In Deep Q Learning, we're specifically trying to minimize the distance between our current Q-value estimate and the Temporal Difference target. Essentially, we are trying to fit the current predicted Q values to the discounted future ones along with the observed rewards.

There are issues that come along with this, though. We will be chasing a non-stationary target, which won't work in practice. Each time we make updates to our Q values, we'll be chasing these updated values during the learning process, a big NO in this supervised approach. How can we correct for this?

Primary Q Network & Target Q Network

In order to overcome the temporal correlation between experiences, we implement 2 networks. The Primary Q Network $Q(s,a;\theta)$ actually learns, while the Target Q Network $Q(s,a;\theta_t)$ is frozen and is used to generate our TD target values, where $\theta$ and $\theta_t$ denotes our model parameters for the primary and target networks, respectively. Having these two makes training more robust, and helps somewhat fix for the issue of chasing a non-stationary target.

In practice, both networks are initialized to the same values. After $N$ training iterations, the parameters from $Q(s,a;\theta)$ are copied over to $Q(s,a;\theta_t)$, and training continues. Essentially, we are introducing some time delay in the update of target Q values during training.

For this Blackjack agent, my inputs to the neural network are similar to those mentioned in my previous post, where we simply pass (player_total, house_value, useable_ace) as inputs. Instead of a boolean for useable_ace, I pass an indicator variable where +1 denotes a useable_ace, and -1 denotes no useable_ace.

Experience Replay

Usually, in reinforcement learning, the agent interacts with the environment, learns from it, then discards those experiences. This is quite inefficient, and leads to temporal correlations, which we're trying to avoid.

In Deep Q Learning, we can make use of a Replay Buffer that stores our experiences in memory. We'll simulate gameplay, store the (state, action, reward, next_state) observations in memory, then sample from these during training. This will de-correlate and sequential experiences and also allow us to learn on batches of prior experiences in an efficient manner.

In practice, I actually use a slight variation of this replay buffer. I'll touch more on this in the following section, but remember that not all actions are available in every state. To account for this, my replay buffer consists of (state, action, action_space, reward, next_state, next_action_space).

We can specificy a maximum alloted size of our experience replay, such that we only remember a certain number of recent observations.

Action Masking

As I mentioned, not all actions are available in each state. There are 2 approaches that I looked into to handle this, one was Implicit Action Masking, the other is Explicit Action Masking.

Implicit Action Masking

With Implicit Action Masking, I can allow the neural network to take any possible action, regardless of whether it's actually in the action space. If it selects an invalid action, then gameplay is immediately stopped (consider it a terminal state), and we can induce some artificial negative reward. The network should be able to learn which actions are valid or not through training.

Explicit Action Masking

In Explicit Action Masking, I can explicitly constrain the output space of the neural network to only those actions that are valid. So, the network won't explicitly learn which actions are viable, but it'll be told which ones are, and we'll never select them. In this explicit approach, let's say our output space is defined as the following, and the output from our Q network are:

$action\_space = ["stay", "hit", "double", "split", "surrender"]$

$Q(s) = [0.2, -0.5, -1, 0.25, -0.5]$

If our viable action space is only $["stay", "hit"]$, then we can mask the output space

$Q(s) = [0.2, -0.5, -\inf, -\inf, -\inf]$

The reason we do this is so when we take an argmax or sample from a softmax of our output space, we are guaranteed to never take these invalid actions. Taking a softmax of $-\inf$ will force the probability of sampling these actions to be $0$.

Tradeoffs

I attempted both methods, and both have their tradeoffs. Originally I went with implicit action masking, as I wanted the network to learn which actions are good vs. bad, and valid at all. However, this requires adding additional inputs to the neural network, such that it has some notion of possible actions to take. The inputs go from (player_total, house_value, useable_ace), to (player_total, house_value, useable_ace, can_split, can_surrender), for example (I remove can_double, as it's implied that whenever we can split, we can also double). Also, we need some additional logic to early stop gameplay when an invalid action is met, and we introduce another hyperparameter to the learning process, as we have to determine a negative reward to force upon invalid actions being taken. I ended up not loving this approach.

Explicit Action Masking ended up working better empirically, and only required minor tweaks to the network to enforce this action masking. I especially preferred this since we didn't introduce another hyperparameter. The only concern I had was that the neural network wouldn't assign low Q values to invalid actions, we just simply ignore them.

Implementation

With the same blackjack modules created for the Q learning approach, I can use them in this deep learning framework. I'll outline some hyperparameters of the learning process

• Replay Size: 10,000
  • Maximum size of our experience replay buffer.
  • Deque structure, so once this maximum size is reached, old observations are removed
• Minimum Replay Size: 1,000
  • Don't begin training until the experience replay buffer reaches this size
• $\gamma$: 0.95
• Target Q Network update frequency: 5,000
  • After this many training epochs, copy the $Q(s,a;\theta)$ parameters over to $Q(s,a;\theta_t)$
• Number of Epochs: 1.5e6
• Batch Size: 16
  • In each training epoch, we minibatch 16 samples from the experience replay buffer
• Action selection: softmax
  • Rather than an $\epsilon$-Greedy sampling approach, I use softmax to determine our actions during training

I use an exponentially decayed learning rate and evaluate the model every 10,000 epochs. The network itself has 3 input dimensions. There are 2 hidden layers of size $[50, 25]$, although this can be experimented with more thoroughly. Instead of a Huber Loss, which I commonly see, I elect to use MSE Loss. For gradient steps, I use the Adam Optimizer.

Replay Buffer

Before we even begin training, we need to populate the replay buffer. At first, this will be completely random, as our neural network is initialized randomly. We do this by simulating gameplay through random action selection, as long as these actions are within the valid action space. In each timestep, we accumulate (state, action_space, action, reward, done, state_next, action_space_next). If state is terminal, then state_next is null, and action_space_next is empty, as well as done being marked as true.

The variable done will denote whether to add the reward to the TD target. If it's not done, we'll force a zero reward, and otherwise, we'll use the reward actually observed from gameplay.

Once we achieve the minimum experience replay buffer size, we can begin learning. In each epoch, we simulate a single round of blackjack. Actions are selected based off our Primary Q Network, where we mask the output space to only valid actions at that timestep, then sample from the Q values for these valid actions using the softmax function. In each epoch, we then sample from our experience replay buffer to train on.

Training

Likely the most confusing step is understanding what we're actually evaluating on when we have both the Target Q Network and the Primary Q Network, as well as action masking.

As we sample from the experience replay buffer in each epoch, we get a tuple of (state, action_space, action, reward, done, state_next, action_space_next). For each state $s$ and action $a$, we can feed this state through our Primary Q Network $Q(s,a,\theta)$, to get our resulting Q values for each action. Then, we can gather the Q value for the specific action $a$ that we took.

Next, we act on the Target Q Network $Q(s,a,\theta_t)$ using our state_next values in order to get our target Q values for each action, then mask them using action_space_next, and take the resulting maximum Q value available. If "done", we use the actual reward found in the replay buffer, otherwise, we force the reward to be zero. We can now establish our TD target by multiplying these target outputs by $\gamma$ and adding the reward.

A simple pseudo implementation of this for a given epoch is shown below. In practice, this is implemented as a minibatch, and the loop won't exist.

1. Simulate gameplay, selecting actions using our primary network and softmax action sampling. Actions are masked before the softmax fuction, according to available actions determined by the gameplay modules.
2. Add these new observations the replay buffer
3. Sample from the replay buffer
4. Use the target network to get the maximum Q value for the next state. We'll use the available action space in order to do so.
5. If the state was terminal, force this value to be zero. Otherwise, use it.
6. Generate our TD target using these target network outputs. Again, if the state wasn't terminal, reward would be zero. Otherwise, we'd observe an actual reward
7. Get the Q value from our primary network for the state, only pulling out the Q value associated with the action taken
8. Calculate loss, update network, repeat.

primary_network = q()
target_network = primary_network
replay_buffer = []

state_action_pairs = simulate(model=primary_network, method="softmax")
replay_buffer.append(state_action_pairs)

samples = sample(replay_buffer)

for sample in samples:
  state, action_space, action, reward, done, state_next, action_space_next = sample

  target_q_values = target_network(state_next)
  target_q_masked = mask(values=target_q_values, mask=action_space_next)
  target_q = max(target_q_masked)
  
  target_q = target_q * (1 - done)

  td_target = reward + gamma * target_q 

  primary_q = primary_network(state)
  primary_q_action = primary_q.gather(action)

  loss(td_target, primary_q_action)

We can gather training losses in each epoch. However, we only evaluate rewards every 10,000 epochs.

Training loss in each epoch. Training seems quite noisy, likely due to the copying of our primary network over to our target network every 5,000 epochs

Average rewards during the evaluation periods throughout training

Evaluation

I don't do as thorough of an analysis on this model compared to my last post, as the main intention was simply seeing whether I could adapt Q learning for a blackjack agent to a deep learning framework.

Value Function

Similar to what I did in my previous post, we can compute the value function for each state. Since the state space is identical to my previous post, the visualization for this feasible to determine, and will look quite similar.

Value function for each state, partitioned by hard totals, soft totals, and ability to split. Some interpolation is done for visual purposes. 'Rewards Distribution` title is misleading.

Compared to my previous post, I think it's fair to say that these Q values and value function are a bit more intuitive. We see better partitioning of states for Soft totals, and the value function peaks more obviously when the house shows a 4-6 compared to a 2-3 across the board.

Conclusion

In this post I outline some fundamentals behind Deep Q Learning, and hopefully detail my specific implementation. I show that I could successfully adapt the Q learning algorithm for in-memory state-action pairs into a deep learning framework, and I get similar if not better results from doing so.

Still, Deep Q Learning is likely an overkill solution to this tractable Q learning problem for blackjack. The state-action space is very limited when we only include (player_total, house_total, useable_ace). In the next post, I'll dive into extending this framework to include card card, and see the performance we're able to achieve...